… Speaker sensativity is frequency independent (that is to say: the crossovers level it). So on, say, a 90db@1w speaker, the tweeter might be intrinsically more sensitive than the woofer; the crossover makes both 90db sensitive.
So [for a non-builder] where does this "extra demand" play out? 110db@40hz will require 100w, as will 110db@20khz. The only exception will be after roll-off starts; but doing custom EQ to compensate for that is really beyond the scope on my question.
To rephrase: does it really require any more power from the amp to generate Xdb at the bottom end of a speaker's flat-response than at the top? If so: what is the math? How is that draw expressed?
To address your questions, I have a few comments.
Speaker sensitivity is expressed as a single number, as if it were constant. But it rarely is. As an example, I chose the Canadian National Research Council's (
NRC) measurements of the B&W 704 s2 speaker. There is no widely accepted standard for measuring sensitivity. It varies significantly among different speaker manufacturers. (Please understand, I am not singling out this speaker as a poor performer. I haven't heard it and I've avoided saying anything about how it sounds.)
The NRC does clearly state their own standard as "averaged 300Hz-3kHz on Listening Window, 2.83V/1m". With the B&W 704, sensitivity was estimated at 87.2dB. A quick glance at its frequency response curve shows a wide range of SPL in that range. This graph shows only the on-axis, 15° and 30° off-axis measurements. The NRC defines its Listening Window as the average of five measurements: on-axis, 15° left and right off-axis, 15° up and down off-axis. So, its clear that sensitivity isn't a constant value across the audio frequency spectrum.
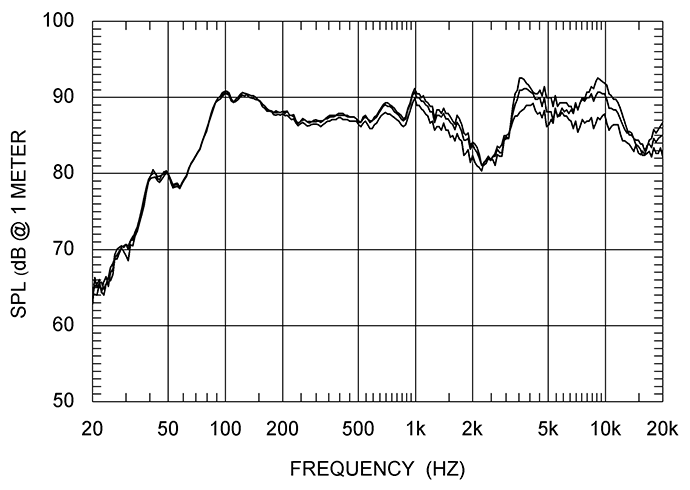
All this is about how speaker sensitivity is measured. It doesn't address how we hear it. We listen to speakers in different locations than where speaker test microphones are placed. We hear a combination of on-axis sound as well as off-axis sound and its room reflections. In the test measurements, the test gear (microphones and software) is set up to maximize sound from one angle while minimizing the others. That's why the NRC defines sensitivity as an average over its listening window.
The NRC's sensitivity numbers average sound from 300 to 3,000 Hz. They avoid speaker response below 300 Hz where room reflections play a large role in how we hear loudness, and where many woofers drop off in loudness becoming more difficult to drive. So when it comes to bass loudness, all bets are off when it comes to speaker sensitivity (at least the way the NRC defines it).
If we can't use speaker sensitivity to judge bass loudness, how can we decide if a speaker is difficult for an amplifier to drive? We have to look at a speakers impedance magnitude in ohms (next graph below),as well as the electrical phase angle of impedance in degrees (below the impedance magnitude graph).
The impedance magnitude shows this speaker's lowest impedance value is below 4 ohms, in the range of 100-200 Hz. In that same frequency range, the phase angle (next graph) shifts quickly from below -45° to above 0°. As the frequency climbs to 1000-2000 Hz, that phase angle continues to increase, reaching as high as +45°. In a speaker with impedance below 4 ohms, this large a phase angle shift of about 90° over a range (100-1000 Hz) that includes the impedance low value, can make it hard for all but the most robust amplifiers to drive.
To summarize, large phase angle shifts when the impedance is low make it difficult for amps to drive speakers loud at those bass frequencies below the NRC's 300-3000 Hz definition of speaker sensitivity. I don't know how to explain in plain English just why this is so (others are welcome to try),but I do know how to look for it in these graphs.
@JerryLove – I hope this helps.